QAM bit error probability for AWGN channel
Assumption: one bit error per symbol error
The bit error probability
of M-QAM over an AWGN channel is given by
(see QAM - Wikipedia)
or
.
See QAM bit error probability calculator and
Error function and Q-function.
|
|
Energy per bit |
|
|
|
Noise power spectral density |
|
|
|
Number of bits per symbol, e.g.
for 4-QAM |
|
|
|
Number of different modulation symbols, size of modulation constellation |
|
Definitions
|
[dB] |
4 QAM
|
16QAM
|
64QAM
|
256QAM
|
| -2 |
1,306E-01 |
1,790E-01 |
1,957E-01 |
1,893E-01 |
| 0 |
7,865E-02 |
1,392E-01 |
1,730E-01 |
1,779E-01 |
| 2 |
3,751E-02 |
9,756E-02 |
1,461E-01 |
1,639E-01 |
| 4 |
1,250E-02 |
5,862E-02 |
1,158E-01 |
1,469E-01 |
| 6 |
2,388E-03 |
2,787E-02 |
8,347E-02 |
1,267E-01 |
| 8 |
1,909E-04 |
9,247E-03 |
5,232E-02 |
1,033E-01 |
| 10 |
3,872E-06 |
1,754E-03 |
2,653E-02 |
7,781E-02 |
Analytical bit error probability
for M-QAM
Note that the real BER is significantly greater than this analytical bit error probability in cases of small
and big M (see marked cells in table). In contrast to the assumption of only one bit error per symbol error, a considerable number of multiple bit errors per symbol error occur in this scenario.
Consider
bit error of symbol errors
The following analytical bit error probability considers a
bit error occurring when non-adjacent constellation points are detected. The probability of this event is added to the probability above.
This approach is a much better approximation in cases of low signal quality. However, the assumption of two bit errors in the case of non-adjacent symbol errors is an approximation as well. In the case of three points further there might be one or three bit errors. Simulation suggests that this bit error probability is an upper limit.
|
[dB] |
4 QAM
|
16QAM
|
64QAM
|
256QAM
|
| -2 |
1,306E-01 |
1,873E-01 |
2,464E-01 |
2,909E-01 |
| 0 |
7,865E-02 |
1,410E-01 |
2,002E-01 |
2,561E-01 |
| 2 |
3,751E-02 |
9,774E-02 |
1,570E-01 |
2,178E-01 |
| 4 |
1,250E-02 |
5,862E-02 |
1,185E-01 |
1,786E-01 |
| 6 |
2,388E-03 |
2,787E-02 |
8,382E-02 |
1,412E-01 |
| 8 |
1,909E-04 |
9,247E-03 |
5,233E-02 |
1,079E-01 |
| 10 |
3,872E-06 |
1,754E-03 |
2,653E-02 |
7,860E-02 |
Analytical bit error probability
for M-QAM considering
bit errors
In this experiment the bit error rate (BER) vs
of M-QAM over an AWGN channel is analyzed.
Quadrature amplitude modulation (QAM) transmission
Start
The simulation starts with 4-QAM and
- see marked cell in table below.
Measured BER approximates the analytical bit error probability
|
[dB] |
4-QAM
|
16-QAM
|
64-QAM
|
256-QAM
|
| -2 |
1,306E-01 |
1,873E-01 |
2,464E-01 |
2,909E-01 |
| 0 |
7,865E-0 |
1,410E-01 |
2,002E-01 |
2,561E-01 |
| 2 |
3,751E-02 |
9,774E-02 |
1,570E-01 |
2,178E-01 |
| 4 |
1,250E-02 |
5,862E-02 |
1,185E-01 |
1,786E-01 |
| 6 |
2,388E-03 |
2,787E-02 |
8,382E-02 |
1,412E-01 |
| 8 |
1,909E-04 |
9,247E-03 |
5,233E-02 |
1,079E-01 |
| 10 |
3,872E-06 |
1,754E-03 |
2,653E-02 |
7,860E-02 |
Analytical bit error probability
for M-QAM considering
bit errors
Experiment
Adjust
and M. Measure the corresponding BER and compare it to the analytical bit error probability.
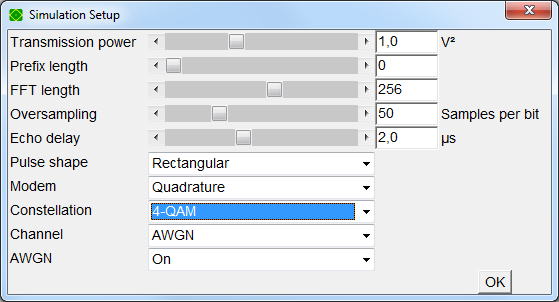
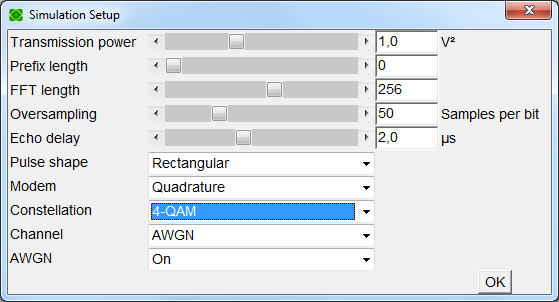
Simulation - Settings (F11)
Simulation - Setup (F12): Set M, the size of the modulation constellation.
Note
- This BER simulation is quite slow as it implements quadrature modulation and pulse shaping.
To boost simulation speed switch to modem none in Simulation - Setup (F12)
- Adjusting
adapts the noise power spectral density. These settings are not modified:
| Transmitting power |
|
| Bit duration
|
|
| Energy per bit
|
|
Next steps
-
The analytical bit error probability
considering
bit errors is a much better approximation in cases of low signal quality.
For instance,
and 16-QAM:
Measured BER
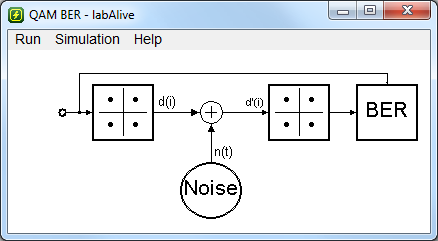
Quadrature amplitude modulation (QAM) transmission
Select the modulation scheme, enter Eb/N0 and start the QAM baseband transmission.
This simulation app implements an M-QAM baseband transmission.
The bit error rate over an AWGN channel can be measured. The baseband simulation is highly performant.
|
QAM modulator demodulator baseband
|
|
Adjust
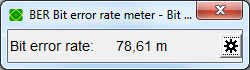
and measure the corresponding BER.
Simulation - Settings (F11)
Simulation - Setup (F12): Set M, the size of the modulation constellation
 To launch labAlive simulation applications you need a Java Runtime Environment supporting Java Web Start on your system. Here you can get more information about installing the right Java version.
To launch labAlive simulation applications you need a Java Runtime Environment supporting Java Web Start on your system. Here you can get more information about installing the right Java version.
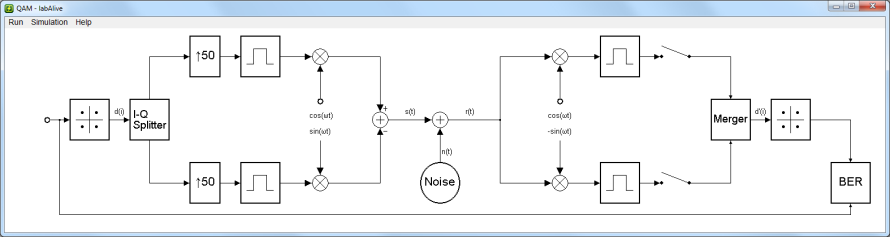

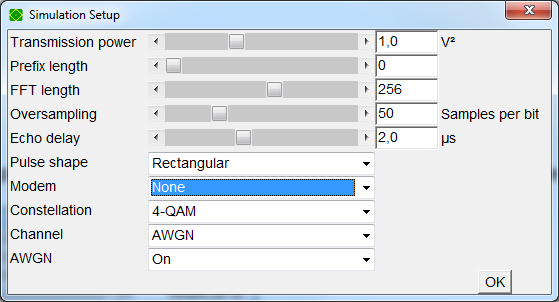 To boost simulation speed switch to modem none in Simulation - Setup (F12)
To boost simulation speed switch to modem none in Simulation - Setup (F12)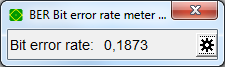 Measured BER
Measured BER