Fast Fourier transform (FFT) - power invariant

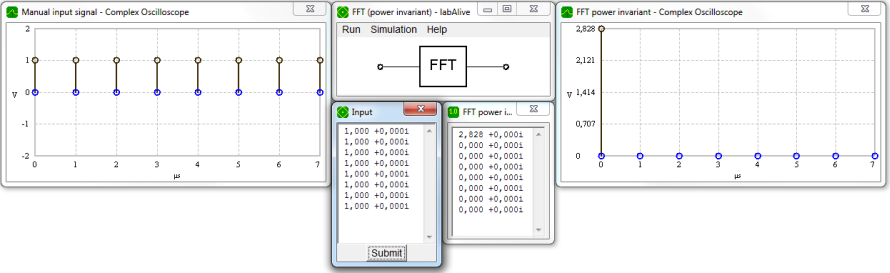
The power of the FFT output signal differs from the input signal power due to an asymmetry in the FFT / IFFT definitions. This FFT variant keeps input and output signal powers equal.

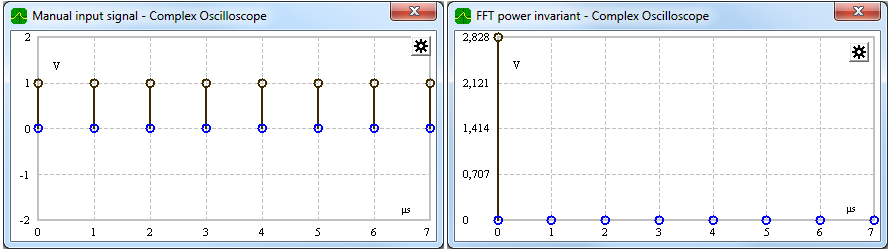
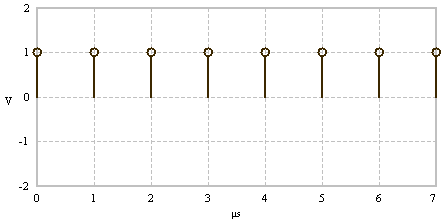
Power invariant Fast Fourier transform (FFT) - time signal (left) and spectrum signal (right) powers are equal.

The FFT transforms a time signal x to a frequency signal X. And vice versa, the IFFT transforms a frequency signal X to a time signal x.

FFT	IFFT
$X_{k} = \sum_{n = 0}^{N - 1} x_{n} e^{- j 2 π k \frac{n}{N}}$	$x_{k} = \frac{1}{N} \sum_{n = 0}^{N - 1} X_{n} e^{j 2 π k \frac{n}{N}}$

FFT / DFT and IFFT / DFT definitions

The spectrum analysis (FFT) and signal synthesis (IFFT) equations look quite similar apart from the term $\frac{1}{N}$ . This asymmetry leads to a power variation of the time and frequency signal. See Fast Fourier transform (FFT)

Power invariant definitions of the FFT and IFFT are shown below. They might be applied in the context of an OFDM transmission in order to not change the signal power by the IFFT and FFT transformations.

FFT	IFFT
$X_{k} = \frac{1}{\sqrt{N}} \sum_{n = 0}^{N - 1} x_{n} e^{- j 2 π k \frac{n}{N}}$	$x_{k} = \frac{1}{\sqrt{N}} \sum_{n = 0}^{N - 1} X_{n} e^{j 2 π k \frac{n}{N}}$

Power invariant definitions of FFT and IFFT

Create your individual signal spectra by using the FFT calculator and check that time and frequency signal powers are equal. Click on the start button above!

Calculate the FFT of real and complex time domain signals. Plot time and frequency signals.

Enter the time domain samples. Press Submit to calculate the frequency domain result.

The data size must be a power of 2: 2, 4, 8, 16, 32...
The format is compatible with Excel: the sequence of complex numbers can be copied from and to spreadsheets.

Note that under this power invariant FFT variation, input and output signal powers are equal.

Enter the time domain data – example formats. Or copy-paste values, e.g. from Excel.

Enter the time domain data - example formats. Or copy-paste values, e.g. from Excel.

Plot time and frequency signals

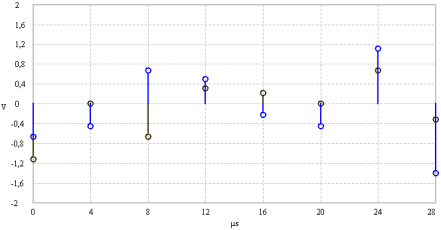
Some examples illustrate the power invariant Fast Fourier transform. Time signals and corresponding frequency signals are shown.

Time domain	Frequency domain
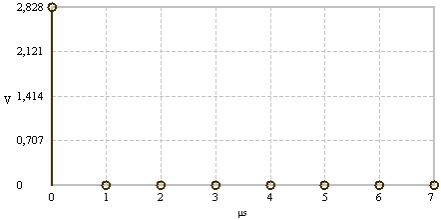
DC component	Spectral line at frequency f=0
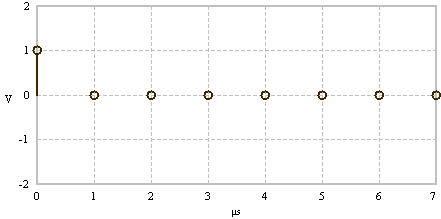
Time signal - Dirac delta impulse	Constant spectrum
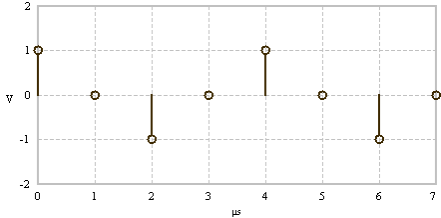
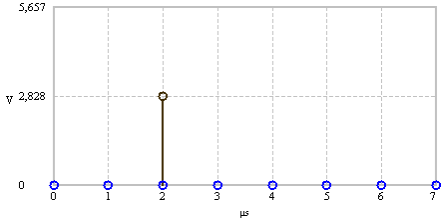
Time signal - cosine with frequency $\frac{f_{\max}}{2}$	Spectral lines at frequencies $\pm \frac{f_{\max}}{2}$
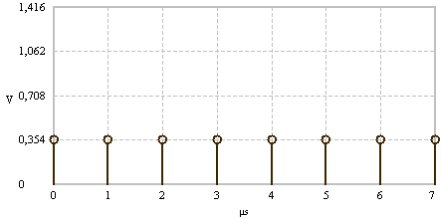
Time signal - cosine with frequency $f_{\max}$	Spectral line at frequency $f_{\max}$

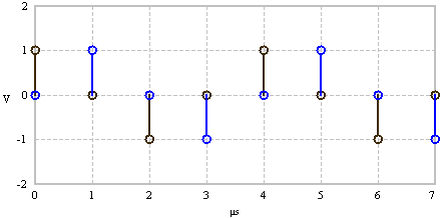
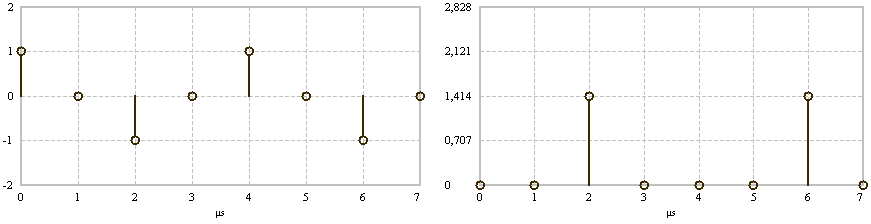
FFT examples (N = 8). The time and frequency domain signals are real and even.

Time domain	Frequency domain
Time signal - pulse	Spectrum signal - Sinc function

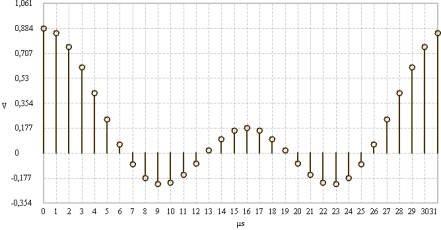
FFT examples (N = 32, power invariant). The time and frequency domain signals are real and even.

Time domain	Frequency domain
Time signal - complex rotating phasor	Single spectral line
Time signal - OFDM symbol	Spectrum signal - OFDM symbol

FFT examples (N = 8). Complex time domain signal.