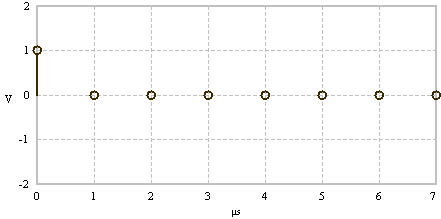
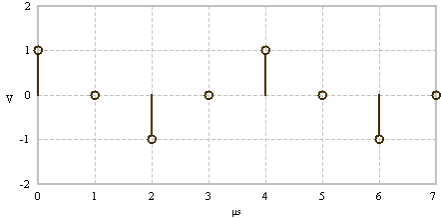
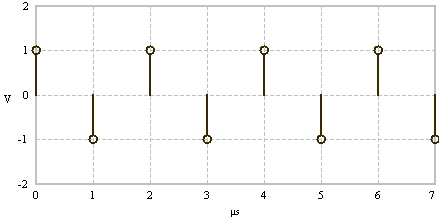
The FFT is an efficient algorithm to compute the discrete Fourier transform (DFT).
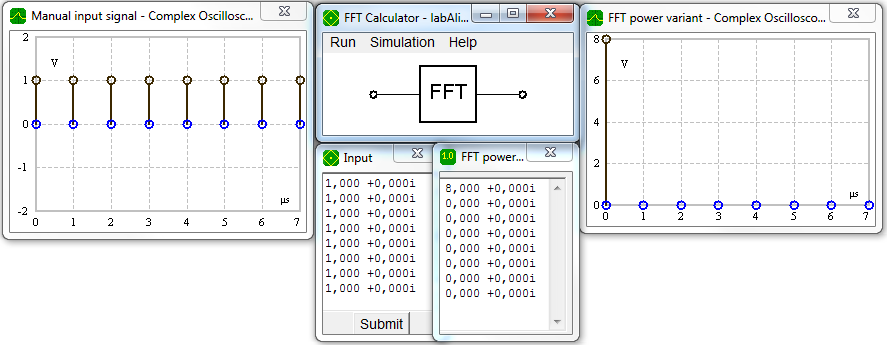
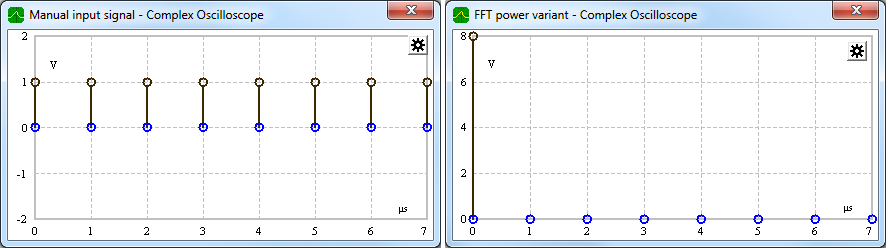
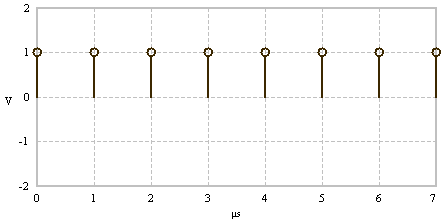
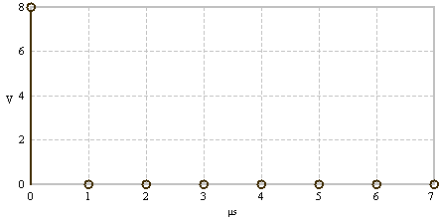
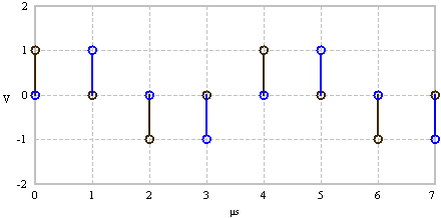
The FFT takes a time signal defined by discrete time points, e.g. N = 8 (left) and computes the spectrum (right).
The FFT transforms a time signal x to a frequency signal X. And vice versa, the IFFT transforms a frequency signal X to a time signal x.
| FFT | IFFT |
|
|
|
FFT / DFT and IFFT / DFT definitions
The spectrum analysis (FFT) and signal synthesis (IFFT) equations look quite similar apart from the term . This asymmetry leads to a power variation of the time and frequency signal.
See also
Create your individual signal spectra by using the FFT calculator.
Click on the start button  above!
above!
Calculate the FFT of real and complex time domain signals. Plot time and frequency signals.
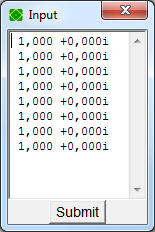
Enter the time domain samples. Press Submit to calculate the frequency domain result.
- The data size must be a power of 2: 2, 4, 8, 16, 32...
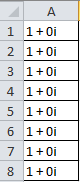
- The format is compatible with Excel: the sequence of complex numbers can be copied from and to spreadsheets.
Enter the time domain data - example formats. Or copy-paste values, e.g. from Excel.
Plot time and frequency signals
Some examples illustrate the Fast Fourier transform. Time signals and corresponding frequency signals are shown.
| Time domain | Frequency domain |
|
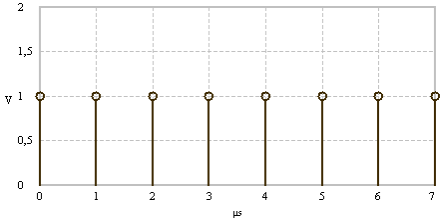
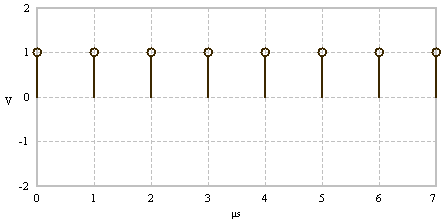
DC component |
Spectral line at frequency f=0 |
|
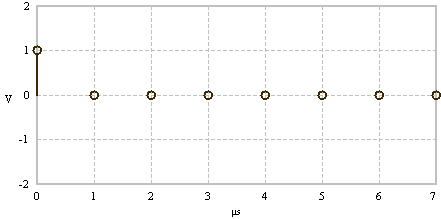
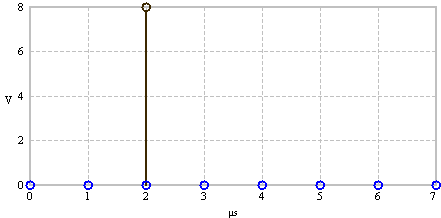
Time signal - Dirac delta impulse |
Constant spectrum |
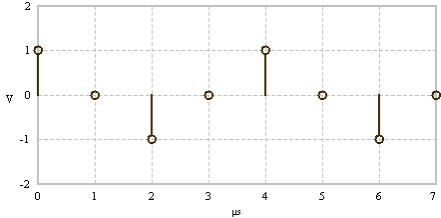
Time signal - cosine with frequency
|
Spectral lines at frequencies
|
Time signal - cosine with frequency
|
Spectral line at frequency
|
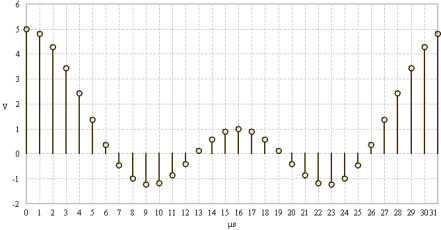
FFT examples (N = 8). The time and frequency domain signals are real and even.
| Time domain | Frequency domain |
|
Time signal - pulse |
Spectrum signal - Sinc function |
FFT examples (N = 32). The time and frequency domain signals are real and even.
| Time domain | Frequency domain |
|
Time signal - complex rotating phasor |
Single spectral line |
FFT examples (N = 8). Complex time domain signal.
 To launch labAlive simulation applications you need a Java Runtime Environment supporting Java Web Start on your system. Here you can get more information about installing the right Java version.
To launch labAlive simulation applications you need a Java Runtime Environment supporting Java Web Start on your system. Here you can get more information about installing the right Java version.
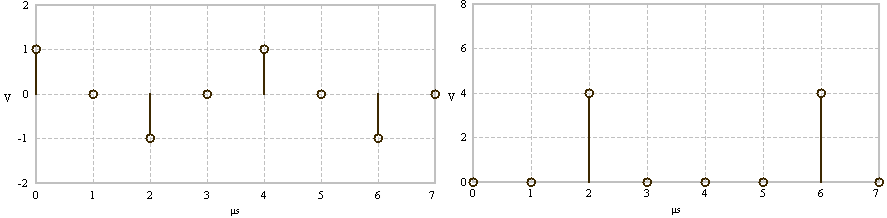
 above!
above!