OFDM loss of Eb/N0 resulting from cyclic prefix and pilot subcarriers
OFDM systems show a loss of Eb/N0 due to the cyclic prefix and pilot carriers.
Effect of cyclic prefix
The last symbols of the OFDM symbol of length are copied and added as cyclic prefix. As the receiver removes the cyclic prefix its energy is lost. This results in a loss of Eb/N0:
Where
Effect of pilot subcarriers
Pilot carriers form an overhead and do not contribute to the user bit rate.
This results in a loss of Eb/N0:
Where
Overall loss
The overall loss of both cyclic prefix and pilot subcarriers is given by
Where
This applies to any modulation scheme. For BPSK and QPSK the BER for AWGN channel is given by:
OFDM systems show a loss of Eb/N0 due to cyclic prefix and pilot carriers, see tutorial.
|
|
Example
In this experiment we analyze a specific IEEE 802.11ac OFDM setup. The theoretical BER for AWGN channel is calculated and compared with simulation results.
The following setting of IEEE 802.11ac is used:
| VHT- MCS Index |
Modulation |
|
|
|
|
Data rate (Mb/s) |
| 800 ns GI |
400 ns GI |
| 1 |
QPSK |
1/2 |
2 |
234 |
8 |
58.5 |
65.0 |
Physical layer parameters IEEE 802.11ac, 80 MHz,
For the 400 ns GI setup the discrete length of the guard interval
is 32. The number of subcarriers is 256. The loss of Eb/N0 yields to
|
|
The effective energy per bit to noise power-spectral-density ratio is . This loss results in a BER degeneration as shown in the following table.
|
in dB |
SC BER |
in dB |
OFDM BER |
| -20 |
4,438E-01 |
-20,658 |
4,478E-01 |
| -15 |
4,007E-01 |
-15,658 |
4,078E-01 |
| -10 |
3,274E-01 |
-10,658 |
3,392E-01 |
| -5 |
2,132E-01 |
-5,658 |
2,305E-01 |
| 0 |
7,865E-02 |
-0,658 |
9,491E-02 |
| 5 |
5,954E-03 |
4,342 |
9,863E-03 |
OFDM shows increased BER compared to single carrier systems (SC) in AWGN channel
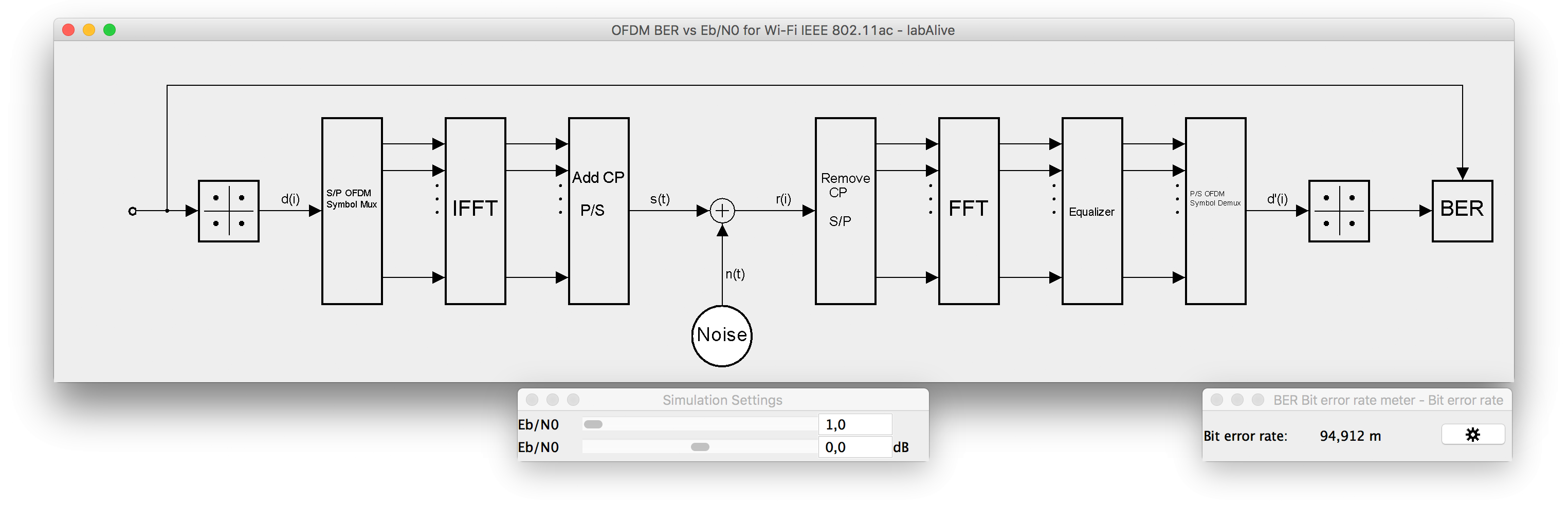
Start
OFDM bit-error rate performance in AWGN channel - block diagram. Implementation of bit error analysis for adjustable E
b/N
0. The Monte Carlo simulation starts with
and approximates the corresponding analytical bit error probability.
Let's first check the Eb/N0 setting.
- The uncoded bitrate is . That's the simulation's bitrate as it doesn't consider coding.
- The transmission power after the symbol mapper is . Unused subcarriers reduce the transmission power:
Measure the transmission power in the simulation!
- The energy per bit yields to
- Noise power spectral density must be set to for .
Check the value of Power-spectral-density N0 of the block Noise in the simulation (click on Noise).
Measure the bit error rate in the simulation!
Adjust Eb/N0 (press F11) and measure the corresponding bit error rate.
Next steps
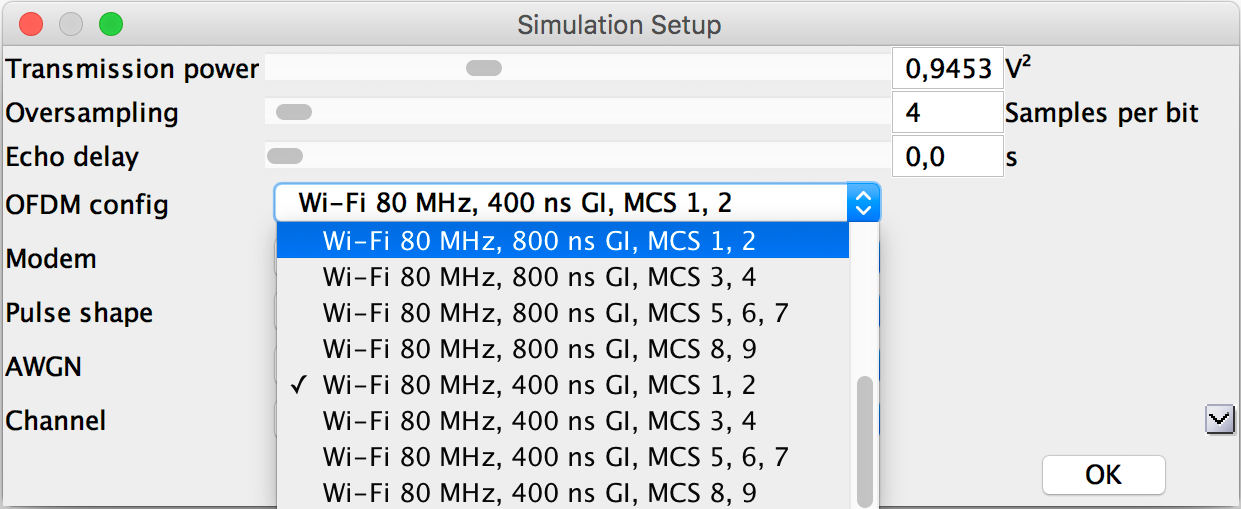
Now select a different OFDM setup: Simulation - Setup (F12). When the guard interval (GI) is increased to 800 ns the loss of Eb/N0 and BER will increase. Calculate and measure the BER analogous to the table above.
This simulation app implements an OFDM transmission using AWGN channel. The bit error rate is measured for variable Eb/N0.
The Monte Carlo simulation starts with
and shows the resulting bit error rate. The parameters of Wi-Fi 80 MHz, 400 ns GI, MCS 1, 2 are used. Different IEEE 802.11ac OFDM schemes can be selected.
| Key |
Action |
Simulation - Settings (F11)

|
Adjust Eb/N0 and measure the corresponding bit error rate. |
Simulation - Setup (F12)
|
Modify the OFDM config and press OK to restart the simulation. |
 To launch labAlive simulation applications you need a Java Runtime Environment supporting Java Web Start on your system. Here you can get more information about installing the right Java version.
To launch labAlive simulation applications you need a Java Runtime Environment supporting Java Web Start on your system. Here you can get more information about installing the right Java version.