Doppler example: Doppler Shift - labAlive experiment

The base station sends a carrier signal

s (t) = \cos (2 π f_{c} t)

. Where

f_{c}

is the carrier frequency.

The wave needs the time $t_{0}$ to reach the car.

The car receives a delayed signal $r (t) = \hat{r} \cos (2 π f_{c} (t - t_{0}))$ .

When the car moves away an additional signal propagation delay occurs.

When the car moves further away an additional signal propagation delay occurs:

t_{1}

Now the car receives the signal $r (t) = \hat{r} \cos (2 π f_{c} (t - t_{0} - t_{1}))$

Where

The initial delay $t_{0}$ causes a constant phase shift $φ_{0} = 2 π f_{c} t_{0}$ .
The car moving away with constant speed $v$ causes an additional, continuously rising delay $t_{1} = \frac{v t}{c}$ .

The received signal yields to:

$r (t) = \hat{r} \cos (2 π f_{c} (t - \frac{v t}{c}) - φ_{0}) = \hat{r} \cos (2 π (f_{c} - \frac{v}{c} f_{c}) t - φ_{0})$

Where we can identify a frequency shift that is known as Doppler shift:

$f_{D} = \frac{v f_{c}}{c}$

Note that an angle between wave propagation and velocity needs to be considered.

The Doppler frequency shift is proportional to the relative velocity and the carrier frequency.

$f_{D} = \frac{v f_{c} \cos (α)}{c}$

Where

$v$ is the relative velocity of sender and receiver.
$f_{c}$ is the carrier frequency.
$α$ is the angle between wave propagation and motion direction.
$c$ is the speed of light.

In channels where transmitter and receiver move relative to each other the signal frequency is shifted depending on the velocity. This so-called Doppler effect can be observed on passing cars, moving stars (redshift of light) and wireless communications.

Start

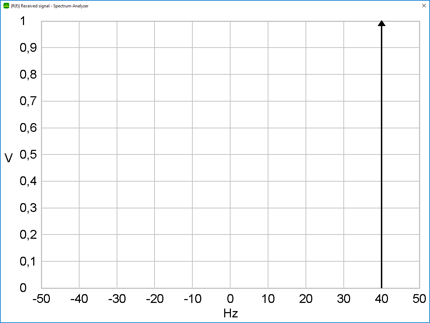
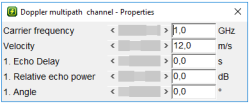
In addition to the video Doppler shift the received signal can be analyzed in the simulation. Start the simulation. Note that the setup is exactly the scenario in the video:

The transmission frequency is 1 GHz.

After the car has accelerated the Doppler shift is 40 Hz in the scenario in the video and this simulation.

Experiment

In the video you were asked to calculate the speed of the car. Now check your result: The car moves with a speed of 12 m/s towards the transmitter.

That can be verified experimentally by changing the speed of the car. Click on Doppler multipath channel in the block diagram. Watch the impact on the Doppler shift.

Furthermore change the angle e.g. 180, 90, 30.

Video Doppler shift: Calculate the speed of the car!

All details you need for doing that are given in the video:

$f_{c} = 1 G H z$
$f_{D} = 40 H z$
$c = 3 \cdot 10^{8} m / s$

The car's speed yields to:

$v = \frac{f_{D} c}{f_{c}} = \frac{40 H z 3 \cdot 10^{8} m / s}{1 G H z} = 12 m / s$

Next Steps

Due to reflections, fading and shadowing there are more transmission paths than the direct one. Think about how the spectrum looks under this condition.

Start the simulation Doppler shift in wireless communications - 2 paths