QAM BER for AWGN channel - labAlive experiment

Optical QPSK Simulation

Simulation of various important transmission parameters

-BASIC CONDITIONS

-MODULATION

-TRANSMISSION ATTENUATION

-DEMODULATION

-OFFSET CORRECTION

-DIFFERENCE TO REAL TRANSMITTION

Basic conditions

This simulation shows how an optical QPSK (quadrature phase shift keying) works with an homodyne receiver (with this modulation type, we can transfer more bits per symbol("2bits")). So we ignore phase shift of the different components, ignore the influence of temperature, use ideal lasers with the exact wavelength and the exact phase for an better comprehension of the theoretical knowledge. The mechanism of action in the optical transmission is that you change the electrical signal into an optical signal with a modulator. Then send it through an optical fiber. The signal is demodulated at the receiver and converted back into an electrical signal by using a photodiode. In this simulation, we use the homodyne transmission. The important thing in this transmission type is the intermediate frequency with 0 difference between the local laser and the receive signal. In a real QPSK, a phase measurement with subsequent phase correction is necessary.

Optical quadrature phase shift keying (QPSK) transmission

Illustration: optical QPSK simulation>

Modulation

The modulator consists of a signal generator, an I/Q splitter, a rectpulse shaper for the I and the Q ways, a local laser and a "Mach-Zehnder-Interferometer" (see Wikipedia) with $L i N b O_{3}$ The signal goes to the I/Q splitter and gets separated into the I way and the Q way. Then it goes into the rectpulse shaper for a defined form and a voltage level on the both ways of the Mach-Zender-Interferometer that is feeded with the local laser. The used effect is that, $L i N b O_{3}$ changes its refractive index (changes the phase) and you can calculate the phase shift with the formula. $φ = \frac{ω_{0} L Δ n_{e f f}}{c}$ In the Q way it is 90� or 270� and in the I way it is 0� or 180�. At the end of the interferometer, we add both ways and produce the four phase shifts( +-45� and +-135�). This signal goes to the optical fiber.

Illustration: optical QPSK modulator>

TRANSMISSION ATTENUATION

In this simulation,we use the transmission attenuation of the optical fiber with the length and the attenuation per km. Further you can add an additional attenuation such as a radius. To keep the simulation easier, we ignore the dispersion and the phase shift of the optical fiber. The transmission can be calculated using the following formulas. $S_{E} = S_{S} * a ² = \hat{r} ² \Rightarrow \hat{r} = \sqrt{S_{S}} * a$ $a = d * m$

DEMODULATION

For the demodulation we split the signal into two ways. To one way you add a local laser with 90� phase shift and to the other way you add a local laser with 0� phase shift. The power is added or subtracted by interference. After mixing, the signals are sent to two photodiodes and are changed into an electrical signal. There is now an electrical Q-signal and I-signal. To form a correlation piont both signals are combined. $c = 10 V; \frac{\hat{c} ²}{2} = 50 V ² \to L o c a l l a s e r = 100 V ² \to L o c a l l a s e r = 20 d B m$ The difference between the optical and the electrical demodulation is, that we add the signal and not multiply it, this is really important. $P_{Q / I} = {(\hat{r} \cos φ_{r} + \hat{c} \cos φ_{c})}^{2} = {\hat{r}}^{2} \cos φ^{2} + {\hat{c}}^{2} \cos φ_{c}^{2} + 2 \hat{r} \hat{c} \cos φ_{r} * \cos φ_{c}$ $A v e r a g e = \int \hat{r} ² \cos (φ_{r}) ² + \hat{c} ² \cos (φ_{c}) ² + 2 \hat{r} \hat{c} \cos (φ_{r}) \cos (φ_{c})$ $A v e r a g e = \frac{{\hat{r}}^{2}}{2} + \frac{{\hat{c}}^{2}}{2} + \hat{r} \hat{c} \frac{\sqrt{2}}{2}$

Illustration: optical QPSK modulator>

OFFSET CORRECTION

Offset correction is important for this modulation type, because light can't have a negative power. The lowest point is zero power. This only exists if the local laser and the received signal eliminate each other completely. So we use the offset correction to set the center for the correlations diagram to zero.

The Offset correction of the optical QPSK is based on the math formula

O f f s e t : \frac{\hat{r} ²}{2} + \frac{\hat{c} ²}{2} = \frac{S_{S}}{2} * a ² + \frac{\hat{c}}{2}

Δ d = \hat{r} \hat{c} \frac{\sqrt{2}}{2} = \sqrt{S_{S}} a \hat{c} \frac{\sqrt{2}}{2}

v * Δ d = \frac{\sqrt{2}}{2} \Rightarrow v * \sqrt{S_{s}} a \hat{c} \frac{\sqrt{2}}{2} = \frac{\sqrt{2}}{2} \Rightarrow v = \frac{1}{\sqrt{S_{s}} a \hat{c}}

Illustration: Constelation diagram without offset

Illustration: Constelation diagram with offset

In this experiment the bit error rate (BER) vs $E_{b} / N_{0}$ of M-QAM over an AWGN channel is analyzed.

Quadrature amplitude modulation (QAM) transmission

Start

The simulation starts with 4-QAM and $\frac{E_{b}}{N_{0}} = 0 d B$ - see marked cell in table below.

Measured BER for 4-QAM, E<sub>b</sub>/N<sub>0</sub> = 0dB

Measured BER approximates the analytical bit error probability

p_{b}

$\frac{E_{b}}{N_{0}}$ [dB]	4-QAM $p_{b}$	16-QAM $p_{b}$	64-QAM $p_{b}$	256-QAM $p_{b}$
-2	1,306E-01	1,873E-01	2,464E-01	2,909E-01
0	7,865E-0	1,410E-01	2,002E-01	2,561E-01
2	3,751E-02	9,774E-02	1,570E-01	2,178E-01
4	1,250E-02	5,862E-02	1,185E-01	1,786E-01
6	2,388E-03	2,787E-02	8,382E-02	1,412E-01
8	1,909E-04	9,247E-03	5,233E-02	1,079E-01
10	3,872E-06	1,754E-03	2,653E-02	7,860E-02

Analytical bit error probability

p_{b}

for M-QAM considering

2^{n d}

bit errors

Experiment

Adjust $E_{b} / N_{0}$ and M. Measure the corresponding BER and compare it to the analytical bit error probability.

Simulation - Settings (F11)

Simulation - Setup (F12): Set M, the size of the modulation constellation.

Note

This BER simulation is quite slow as it implements quadrature modulation and pulse shaping.

To boost simulation speed switch to modem none in Simulation - Setup (F12)

Adjusting

E_{b} / N_{0}

adapts the noise power spectral density. These settings are not modified:

Transmitting power	$1 V^{2}$
Bit duration $T_{b i t}$	$1 μ s$
Energy per bit $E_{b}$	$1 μ V s^{2}$

Next steps

The analytical bit error probability $p_{b}$ considering $2^{n d}$ bit errors is a much better approximation in cases of low signal quality. For instance, $E_{b} / N_{0} = - 2 d B$ and 16-QAM: $p_{b} = 0,1873$

Measured BER

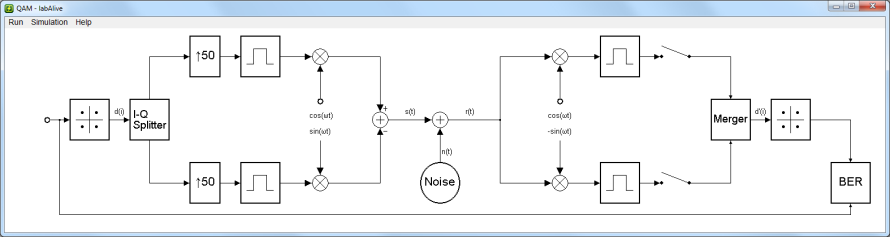
Quadrature amplitude modulation (QAM) transmission

Select the modulation scheme, enter E_b/N₀ and start the QAM baseband transmission. This simulation app implements an M-QAM baseband transmission. The bit error rate over an AWGN channel can be measured. The baseband simulation is highly performant.